The Team

Andrew, Krinal, Kyle, Max, Simon

Introduction

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector space, allowing us to view a group as a collection of linear maps on a vector space. Group theory is hard, so this allows us to tackle problems in group theory by doing linear algebra instead, which is a well understand subject and one for which we have developed many powerful tools.

Each element in a group is assigned some matrix, for example the identity element of a group is assigned the identity matrix, and these matrices must respect the same relationships as their corresponding elements in the group. A collection of such matrices is what we consider the representation of a group.

Representations allow us to view a simplified version of the group, preserving some important information but stripping the rest. This allows us to gain a sense of its properties without needing to comprehend the full complexity of a given group. A group can have multiple representations, and each presents slightly different information about the group.

Representation theory has a diverse set of applications; in addition to its uses in abstract algebra, it sees many applications in physics. Specifically, in the application of representation theory to Lie groups, the structure of which are linked to the properties and behavior of elementary particles. Additionally, representation theory and harmonic analysis are intimately related, with representation theory generalizing Fourier analysis via harmonic analysis,

History

Representation theory arises on April 12, 1896 when Frobenius penned his first letter to Dedekind describing his new ideas on factoring a certain homogenous polynomial associated with a finite group called the "group determinant". Further letters quickly ensued, and by the end of the month Frobenius had the rudiments of the character theory of finite groups.

It would take more time for the concept of group representations to be fully developed, but this dialogue in April is what most historians hail as the single most significant event marking the birth of representation theory.

In the twenty remaining years of Frobenius's life, he would go on to write over a dozen additional papers in group theory, beyond the initial two, further developing the theory of group characters and group representations and applying these to finite group theory, including the definition of a group representation as we understand it in modern theory (albeit somewhat clunkily).

His work would go on to provide the basic tools for various branches of algebras, and their generalizations beyond play important roles in further fields of mathematics. Group characters and representations also have come to be used, decades later, extensively in a wide range of applied fields, including spectroscopy, crystallography, quantum mechanics, and more.

Application

Representation theory is a natural way of extending the ideas of groups from a purely algebraic idea to other mathematical objects. In algebra we learn that groups are defined purely by their abstract group actions. However, in practice, there are many things that may exhibit group properties. These things include manifolds, polynomial equations, differential equations, and even molecules. Such things are naturally defined by vector spaces, however they have actions that can be expressed as a group. This is where representation theory can come into play. Contrary to some beliefs, Representation theory is not just to find or create representations, ‘it is to study the structure of such (group) actions and how they behave under operations of linear algebra’ - how a group can act on a vector space. Primarily, once a linear representation is created, what is the limit as to how far one can simplify it, how can one identify when a simpler representation exists, and how can we classify when a representation is irreducible

Mobius Transformations

Groups by themselves are not very insightful or easy to understand. They are just a collection of identities and rules that define what happens when two elements are put together. What we are really interested in are the group actions, or how the group acts on a given set. With this extension, it gives the group a new meaning, and makes the problem much more manageable. Say we are given the abstract representation of some arbitrary group, how should we begin to study it? One way is to try to find homomorphisms of this group which map to other groups which have well known representations. Say we are given an abstract group G, and we find a homomorphism onto the group defined by the set of invertible 2x2 matrices with complex entries

$\begin{bmatrix} a & b \\ c & d\end{bmatrix}$ This group is known as the general linear group. Now some questions may arise; what are the natural actions of our group, what kind of objects and symmetries are we dealing with?

Claim: There exists a group homomorphism from $GL(2, \mathbb{C})$ under matrix multiplication onto the Mobius Transformations under function composition.

For background reference, Mobius Transformations are the class of functions on the complex plane which are made up of compositions of rotations; $w = e^{i\phi}z$, $\phi \in [0, 2\pi)$, magnifications; $w = \rho z$, translations; $w = z + c$, and inversions $w = \frac{1}{z}$. They are linear fractional transformations and they look as such; $f(z) = \frac{az + b}{cz + d}$ They form a group under function composition. All of these facts can be proven using basic algebra.

Proof of claim: This map can be made by taking the entries of the matrix and making them coefficients of the linear fractional transformation

Let $\begin{bmatrix} a & b \\ c & d\end{bmatrix} \rightarrow f(z) = \frac{az + b}{cz + d}$ and $\begin{bmatrix} e & f \\ g & h\end{bmatrix} \rightarrow g(z) = \frac{ez + f}{gz + h}$

$\begin{bmatrix} a & b \\ c & d\end{bmatrix} \cdot \begin{bmatrix} e & f \\ g & h\end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh\end{bmatrix}$

$f(g(z)) = \frac{a(\frac{ez + f}{gz + h}) + b}{c(\frac{ez + f}{gz + h}) + d} = \frac{\frac{a\left(ez+f\right)+b\left(zg+h\right)}{zg+h}}{\frac{c\left(ez+f\right)+d\left(zg+h\right)}{zg+h}} = \frac{a(ez+f)+b(zg+h)}{c(ez+f)+d(zg+h)}= \frac{(ae + bg)z + (af + bh)}{(ce + dg)z + (cf + dh)}$

Thus, multiplying matrices maintains the structure similarly to function composition.

An important observation is that all of these functions are one-to-one and onto on the whole extended complex plane, and all are analytic in the whole extended plane with the exception of $\frac{1}{z}$ at 0. So, the map $f(z) = \frac{az + b}{cz + d}$ is one-to-one, onto, analytic, and conformal in the whole plane minus one point. (This can take a whole semester of complex analysis to prove so I will omit the justification for this claim.)

Great! Now we know that these groups have a similar structure and have a homomorphism;

$\pi : GL(2, \mathbb{C}) \rightarrow Aut(\hat{(\mathbb{C)}})$

However, there is a slight issue with this. It is clear that multiplying the function by scalar of the form $\frac{c}{c}$, will leave function unchanged, but will change the representation matrix. Thus, we can say this transformation has a kernel of all identity matrices who differ by a scalar. Then, by the first isomorphism theorem, the quotient group $GL(2, \mathbb{C}) / (\bar{\mathbb{C}} / 0 \cdot I) \cong Aut(\hat{\mathbb{C}})$ This quotient group has a special name, and it goes by the projective general linear group.

In other non math heavy words, the issue with having $GL(2, \mathbb{C})$ be mapped directly to the Mobius group is that if we have a mobius transformation being represented by a matrix $A$, it turns out that there exists infinitely many matrices that represent the transformation. Consider a scalar $c\in \mathbb{C}$, it is clear that when $A = cB$, $A, B$ represent the same thing. We can reduce this ambiguity by ensuring that the matrices have a determinant of 1. The only problem left is that $A, -A$ both have the same determinant and both represent the same group; however, this is a massive improvement in comparison to what we had before.

The set of matrices of determinant 1 is called the special linear group, and the set of Mobius transformation is called the Projective special linear group which is isomorphic to the Projective linear group. It is said that the Special Linear Group is a double cover of the Projective Special Linear Group. This is a type of problem that is dealt with a subject called Projective Representation Theory

Now back to the original question, what are some of the geometric behaviors of this group? One of the main selling points of representation theory was that representing a group as a matrix could provide some additional, possible geometric insights. Luckily for us, matrices have a very beautiful geometric structure on vector spaces .

Riemann Sphere

I will do this is by something called a stereographic projection. It is a function, which uniquely maps each point on a sphere onto a plane. In our case, we will want to map a 3 dimensional sphere onto the complex plane. This map is not isometric, which means it does not preserve distances or areas. However, it is conformal, which means it preserves angles.

Now, my claim is that one can map the unit 3 sphere onto the complex plane in a one-to-one fashion.

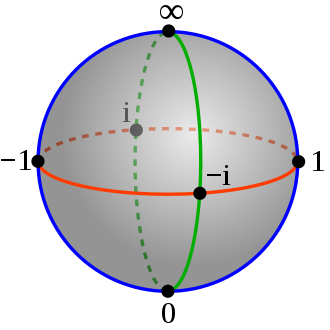
Claim: There exists a projection of the unit sphere $(x_1, x_2, x_3)$ onto the complex plane $z = x + iy$ via the map $x_1 = \frac{2x}{|z|^2 + 1}, x_2 = \frac{2y}{|z|^2 + 1}, x_3 = \frac{|z|^2 - 1}{|z|^2 + 1}$

Proof of claim: If $Z = (x_1, x_2, x_3)$ are points on the Riemann sphere, then they get mapped to a unique point $z = x + iy$.

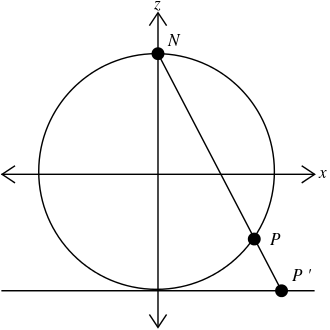
I will do this by first considering a line of negative slope passing through the top of the sphere, let that point be $N = (0, 0, 1)$, and the point $(x, y, 0)$ on the complex plane. This can be given by the parametric equations; $x_1 = tx, x_2 = ty, x_3 = 1 - t, -\infty < t < \infty$ This line intersects the sphere when t satisfies; $1 = x_1^2 + x_2^2 + x_3^2 = t^2x^2 + t^2y^2 + (1 - t)^2$ or more simply $1 = t^2(x^2 + y^2 + 1) + 1 - 2t$

whose roots are $t = 0$ (north pole) and $t = \frac{2}{x^2 + y^2 + 1} = \frac{2}{|z|^2 + 1}$. Plugging in this value of $t$ gets the map mentioned above.

The inverse map would then be $x = \frac{x_1}{1 - x_3}, y = \frac{x_2}{1 - x_3}$

Now, knowing that the Riemann sphere is 1-1 to the extended complex plane, we may conclude that the Mobius group acts on the sphere.

But, this map does not preserve distance in the usual sense, so one might ask what are the symmetries of the Mobius group on this sphere. Well, some investigation into the sphere might lead to some answers.

Claim: All lines and circles on the complex plane are just circles on the Riemann Sphere

Proof of claim: The general equation for a line or a circle in the complex plane is given by: $A(x^2 + y^2) + Cx + Dy + E = 0$ for $z = x+iy \in \mathbb{C}$.

Now, substituting the results of our previous proof;

$A[(\frac{x_1}{1 - x_3})^2 + (\frac{x_2}{1 - x_3})^2] + \frac{Cx_1}{1 - x_3} + \frac{Dx_2}{1 - x_3} + E = 0$

Which may be simplified to;

$A(x_1^2 + x_2^2) + Cx_1(1 - x_3) + Dx_2(1 - x_3) + E(1 - x_3)^2 = 0$

Then, because $x_1, x_2, x_3$ all lie on the sphere, we can use the identity $x_1^2 + x_2^2 + x_3^2 = 1$ to rewrite the equation in terms of $x_3$;

$A(1 - x_3^2) + Cx_1(1 - x_3) + Dx_2(1 - x_3) + E(1 - x_3)^2 = 0$

Then, dividing by $(1 - x_3)$ gets;

$A(1 + x_3) + Cx_1 + Dx_2 + E(1 - x_3) = 0$

or

$Cx_1 + Dx_2 + (A - E)x_3 + A + E = 0$

Which of course, is the equation of a plane in 3 dimensional space.

Thus, I have shown that any line or circle in the complex plane must lie in a plane, as well as the Riemann sphere. And thus, an intersection of a plane and a sphere is of course a circle.

Then, from geometry we know that 3 points in a plane can either be collinear, or they aren't. When they are not collinear there exists a unique circle which hits each of them. Thus, 3 points are either a line or a circle, and thus they are all circles on the Riemann Sphere.

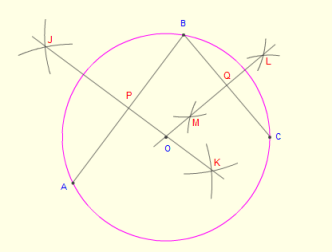
With a little more effort, it can be shown that given any 3 points $z_1, z_2, z_3$ in the $z$ complex plane, and 3 points $w_1, w_2, w_3$ in the $w$ complex plane, there exists a unique Mobius transformation between them.

Therefore, we now know that the set of Mobius transformations are the set of functions which map the entire complex plane onto itself, and it maintains the symmetry of mapping generalized circles to generalized circles!

So, when we started with an abstract group, if we can prove that it has a group homomorphism with the set of invertible 2x2 complex matrices, we can begin to understand everything about the group, including its actions on a sphere and a 2-D plane, its symmetries on these objects, and other groups with a very similar structure!

Dirchlet Problem

A more concrete understanding on the importance of the Möbius Transformations is through its application in solving Dirichlet Boundary value problems. Many physical concpets in engineering and physics use the Laplace equation - $\frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} = 0$ Particularly the model stream lines, Temperature distributions, electric potentials.

The theorem used to achieve this is the following - Suppose that w = (z) is an analytic function on some open set $D_w$ and its image is another open set $D_x$. If $h(x,y)$ is harmonic on $D_w$ then $H(x,y)$ := $h(u,v)$ is harmonic function

This theorem effectively allows us to reduce Solving Boundary condition problems to solving mapping problems as we can find a generalized solution to one and then find transformations of any domain to the generalized solution.

Euclidean Group

One of the oldest and most studied Groups is the Euclidean Group. It is a Group isometric system that preserves the Euclidean Distance between any two points. They are entirely dependant on the number of dimensions.
Some examples are -
$t_A$ translation of origin to point A
$\rho_A(\theta)$ Rotation by $\theta$ around point A
$r_l$ reflection in the line l

It has as subgroups the translational group T(n), and the orthogonal group O(n). Any element of E(n) is a translation followed by an orthogonal transformation (the linear part of the isometry), in a unique way:

$x \mapsto A(x + b)$ where A is an orthogonal matrix

or the same orthogonal transformation followed by a translation:

$x \mapsto Ax + c$ with $c = Ab$

T(n) is a normal subgroup of E(n): for every translation t and every isometry u, the composition

$u^{−1}tu$ is again a translation.

Summary

In conclusion, representation theory is a very rich branch of mathematics that an be applied to numerous other fields to enhance one’s understanding. By enabling mathematicians to examine algebraic structures using the well understood techniques of linear algebra, we are able to explore and solve problems inaccessible with the conventional methods of those respective fields. These applications range from usages in physics in quantum mechanics and quantum field theory, number theory and combinatorics, Fourier/harmonic analysis, and more. Its flexibility of application across fields and the ability to approach it from a diverse set of angles all contribute to representation theory’s pervasiveness through mathematics as a whole