1.Theory and Background:

Bateman–Burgers equation is a fundamental partial differential equation and convection–diffusion equation occurring in various areas of applied mathematics, such as fluid mechanics, nonlinear acoustics, gas dynamics, and traffic flow.

$\frac{du}{dt} + u\frac{du}{dx} = \frac{d^2u}{dx^2}$

$u_t +uu_x - (0.01/\pi)u_{xx}= 0$

$u(0,x)=-sin(\pi x)$ $u(t,-1)=u(t,1)=0$

2. Traditional Methods vs. Neural Networks

Traditional Methods	Neural Networks
Finite Difference: Approximates derivatives using small finite differences.	Flexible Approximators: Neural networks can approximate complex nonlinear functions, making them suitable for solving a wide range of partial differential equations.
Finite Element: Divides the domain into smaller elements, approximating the solution within each element and assembling them into a global system of equations.	Computational Efficiency: Neural networks can offer computational efficiency by bypassing the need for explicit mesh generation and discretization, making them attractive for real-time or large-scale simulations.
Spectral Methods: Represent the solution as a sum of basis functions, such as trigonometric or polynomial functions, providing high accuracy but limited to specific geometries.

3. Architecture:

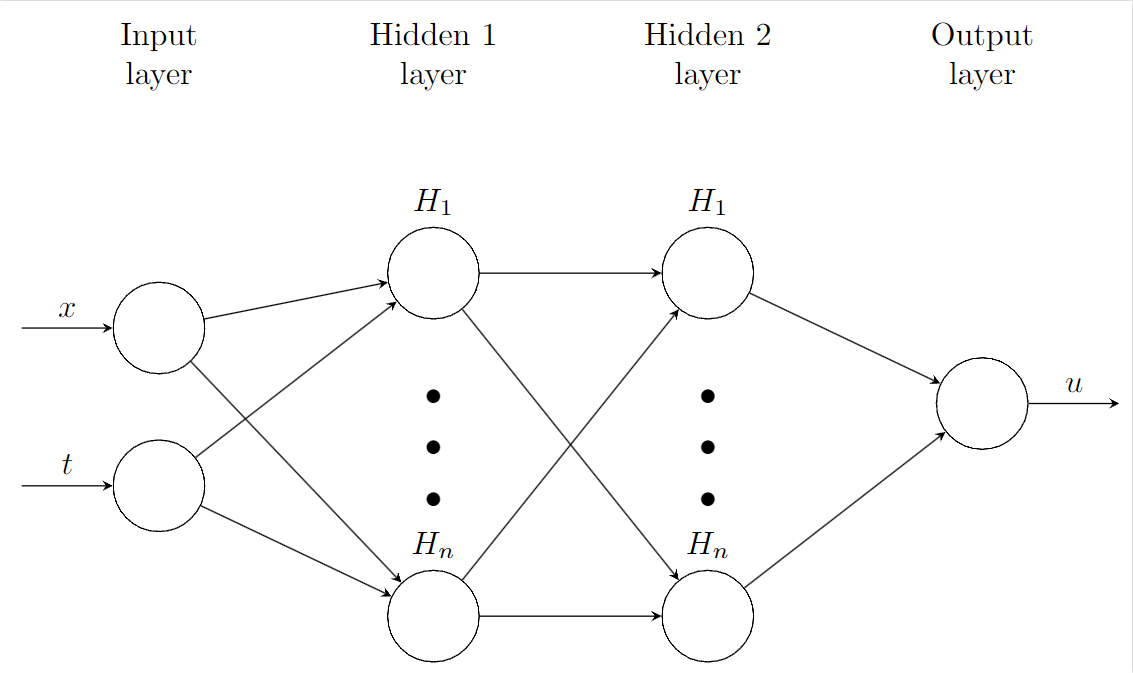
An image of the neural net architecture

4. Results and Discussion:

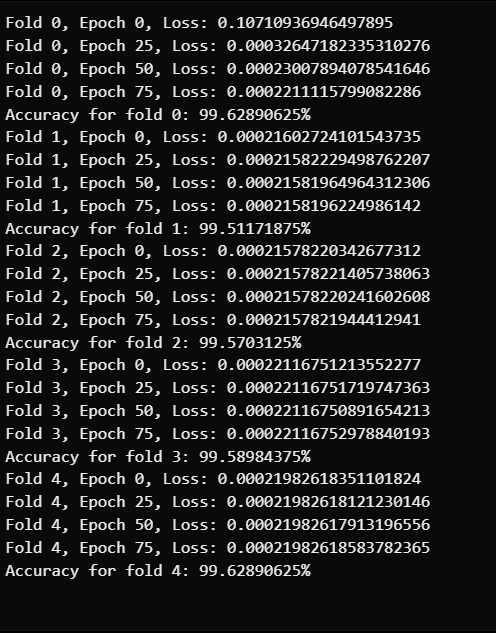
List of Loss on Epochs

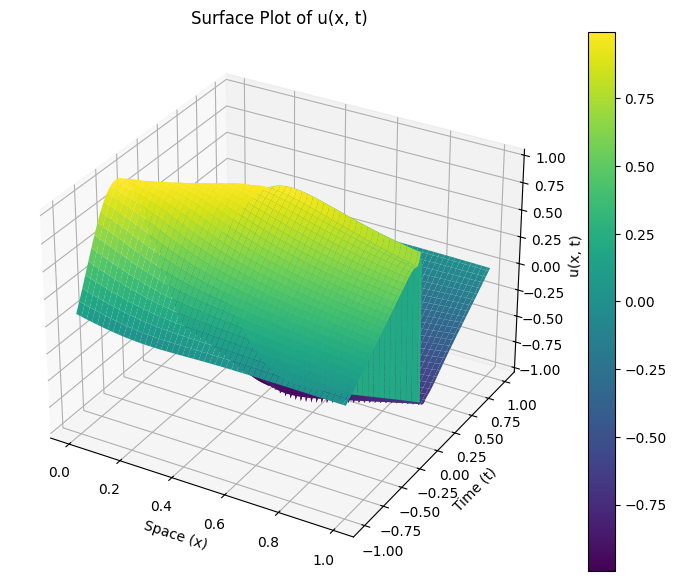
Graph of the function

5. Applications and Future Work

Neural Networks can be used as an alternative to numerical methods

Hyperparameter tuning for compute Efficiency
Robustness in architecture by varying training data
Solving Discrete Time Models
Full Vortex Simulation with hyperparameters